5 NAPÄŤOVÁ A PRÚDOVÁ SPÄTNÁ VÄZBA
Ak sa z výstupu zosilňovača odoberie časť jeho zosilneného signálu (napätie alebo prúd) a privedie sa na vstup, označujeme toto riešenie ako spätnú väzbu.
Podľa veľkosti fázového posunu medzi pôvodným signálom a signálom privedeným z výstupu sa výsledný prenos buď zmenšuje ( vtedy hovoríme o zápornej spätnej väzbe) , alebo zväčšuje ( vtedy hovoríme o kladnej spätnej väzbe).
Záporná spätná väzba zmenšuje vstupný signál, harmonické, frekvenčné aj fázové skreslenie, ovplyvňuje vstupnú a výstupnú impedanciu, veľkosť rušivého napätia a zmenšuje citlivosť zosilňovača na zmenu parametrov tranzistora.
Kladná spätná väzba pôsobí na spomínané parametre zosilňovača vo väčšine prípadov opačne ako záporná spätná väzba, navyše za určitých podmienok mení zosilňovač na oscilátor.
Môžeme povedať že spätná väzba je frekvenčne závislá, pretože zosilňovač v určitom pásme frekvencií má zápornú spätnú väzbu a v inej frekvenčnej oblasti kladnú spätnú väzbu.
Preto pri zosilňovači so spätnou väzbou je najväčším problémom jeho stabilita, t.j. odolnosť proti rušivému samočinnému kmitaniu.
[5.1][5.2]
V závislosti od toho, akým spôsobom je
Na vysvetlenie vplyvu spätnej väzby na vlastnosti zosilňovača použijeme sériovo napäťovú spätnú väzbu.
Na vstupe zosilňovača so spätnou väzbou pôsobí napätie:
po úprave rovnice (5.4) a dosadení za U1 do vzorca (5.3) dostaneme pre zosilnenie so spätnou väzbou:
kde ß.A - je stupeň spätnej väzby.
Môže nadobúdať rôzne hodnoty kladné aj záporné a vzhľadom na to môžu nastať tieto prípady:
kde φA a φß sú fázové posuny spôsobené samotným blokom zosilnenia a blokom spätnej väzby.
Potom zosilnenie zosilňovača so spätnou väzbou môžeme vyjadriť:
Ak bude platiť, že φA + φß = π = 180°, bude ß.A = - ß.A, takže ide o reálnu a zápornú hodnotu.
Spätnej väzbe, ktorá využíva túto skutočnosť hovoríme záporná spätná väzba.
Z predchádzajúcej rovnice vyplýva, že zosilnenie zosilňovača so zápornou spätnou väzbou je vždy ( 1+ßA )-krát menšie ako zosilnenie zosilňovača bez spätnej väzby.[5.1]
Blackov vzťah zýskame nasledovným odvodením z obr.5.1, ktorý je:
A'ex - je externý prenos napätia zo zdroja na výstup zosilňovača
Stabilita zosilnenia zosilňovača
Stabilitou zosilnenia rozumieme mieru zmeny zosilnenia k celkovému zosilneniu zosilňovača. Vyjadrujeme ju pomerom
alebo pre veľmi malé zmeny v tvare
Ak rovnicu (5.3) derivujeme podľa zosilnenia A, dostaneme:
Z tejto rovnice vyplýva, že stabilita zosilnenia zosilňovača so zápornou spätnou väzbou sa zlepší,
lebo celková miera zmeny zosilnenia je ( 1 + ßA ) - krát menšia ako u zosilňovača bez spätnej väzby.[5.1]
Stabilita zosilňovača
Nedostatkom zosilňovača so spätnou väzbou je možnosť vzniku parazitných kmitov na výstupe a to aj v tom prípade, keď na vstupe nepôsobí žiadny signál.
Preto prenos bloku zosilnenia A a prenos bloku spätnej väzby ß sú vo všeobecnosti komplexné čísla a platí:
a ich súčin:
Pri splnení podmienky φA + φß = 2kπ ;kde k=0,1,2,... platí, že A.ß=|Aß|
ide teda o kladnú spätnú väzbu. Ak sa splní ešte aj podmienka, že súčin A.ß > 1, vznikajú v obvode zosilňovača samočinné kmity, oscilácie.
Lepšiu predstavu o stabilite zosilňovača so spätnou väzbou dostaneme, ak ho chápeme ako regulovanú sústavu.
Stabilitu regulovaných sústav určujeme podľa viacerých kritérií (imitančné, Hurwitzovo, Nyguistovo).
Najznámejšie je Nyguistovo kritérium stability, pretože umožňuje nielen kvalitatívne, ale aj kvantitatívne posúdenie stability zosilňovača.
Ďalšou skutočnosťou, ktorá prispieva k nestabilite zosilňovača so zápornou spätnou väzbou ako celku je aj to, že prenos A bloku zosilnenia a prenos ß bloku spätnej väzby sú frekvenčne závislé. Súčin A.ß môžeme vyjadriť v komplexnom zložkovom tvare:
Dosadením rôznych frekvencií od 0 do ∞ môžeme určiť pre každú frekvenciu zložky a(f) a b(f) a vyniesť ich do grafu v Gaussovej rovine.
Modul |Aß| a argument φ pre danú frekvenciu dostaneme z nasledujúcich rovníc:
Spojením koncových bodov fázora |Aß| pre frekvencie od 0 do ∞, dostaneme krivku stability.
Bod [1,0] je bod stability a platí:
Z týchto poznatkov môžeme povedať, že zavedením zápornej spätnej väzby do obvodu zosilňovača sa jeho stabilita ako celku zhorší.
[5.1]
Činiteľ frekvenčného skreslenia
Všimnime si ako sa zmení frekvenčná charakteristika zosilňovača, teda činiteľ frekvenčného skreslenia.
Pre zosilňovač bez spätnej väzby je činiteľ frekvenčného skreslenia kf rovný :
a pre zosilňovač so spätnou väzbou je činiteľ frekvenčného skreslenia rovný
AS - je zosilnenie zosilňovača bez spätnej väzby pre stredné frekvencie
Vieme, že:
Ak dosadíme tieto vzťahy do rovnice (5.21), dostaneme:
a keďže Ad < AS, potom k'f < kf , teda v zosilňovači so zavedenou zápornou spätnou väzbou je činiteľ frekvenčného skreslenia k'f menší ako v zosilňovači bez spätnej väzby.
Táto skutočnosť sa dá vyčítať aj z frekvenčných charakteristík zosilňovača so spätnou väzbou a bez nej, ako to vidíme na obrázku.
Na obrázku môžeme vidieť, že so zavedením spätnej väzby sa nielenže zmenší frekvenčné skreslenie, teda sa vyrovná frekvenčná charakteristika, ale sa zväčší aj šírka prenášaného pásma pre pokles o 3 dB.
Činiteľ harmonického skreslenia
Činiteľ harmonického skreslenia k'h v zosilňovači so zápornou spätnou väzbou je ( 1 + ßA ) - krát menší ako u zosilňovača bez spätnej väzby.
Tento vzťah má však obmedzenú platnosť. Vzťah je použiteľný ak platí, že:
Vo všeobecnosti môžeme povedať, že spätná väzba mení vstupnú a výstupnú impedanciu pôvodného zosilňovača.
V prípade paralelnej spätnej väzby platí:
Pre prúdovú spätnú väzbu platí:
a pre napäťovú spätnú väzbu:
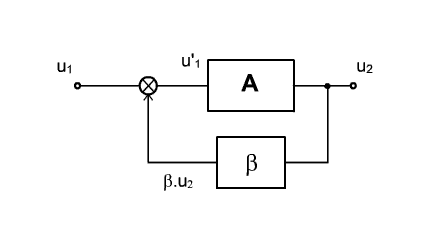
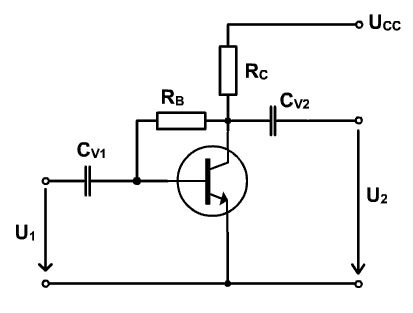
Obr. 5.1 Principiálna bloková schéma spätnej väzby
Blok označený písmenom A sa nazýva blok zosilnenia.
Blok označený písmenom ß sa nazýva blok spätnej väzby.
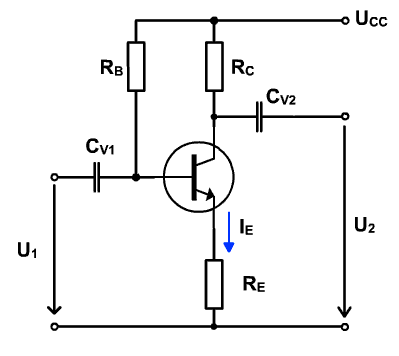
Obr. 5.2 Blokové schémy jednotlivých typov spätných väzieb
5.1 Základná teória
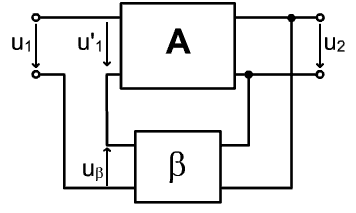
Obr. 5.3 Sériová napäťová spätná väzba
Najskôr si zadefinujeme základné vzťahy a pojmy.
Blok označený písmenom A predstavuje zosilňovač s prenosom :
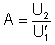
![]() (5.1)
(5.1)
Blok spätnej väzby ß je obvykle tvorený pasívnymi prvkami a preto výstup z neho Uß predstavujú iba zlomok signálu privedeného na jeho vstup.
Vo všeobecnosti platí:
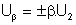
![]() (5.2)
(5.2)
kde ß - je činiteľ spätnej väzby.
Môže nadobúdať hodnoty od 0 do +1 pri kladnej spätnej väzbe a od 0 do -1 pri zápornej spätnej väzbe.
Zosilnenie zosilňovača ako celku so zavedenou spätnou väzbou je:
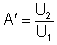
![]() (5.3)
(5.3)
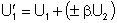
![]() (5.4)
(5.4)
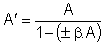
![]() (5.5)
(5.5)
ß.A = 1....... vznik harmonických oscilácií
ß.A > 0....... kladná spätná väzba
ß.A < 0....... záporná spätná väzba
ß = 0.......spätná väzba neexistuje
Vo všeobecnosti sú A a ß komplexné čísla, môžeme ich vyjadriť v komplexnom tvare:
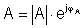
![]() (5.6)
(5.6)
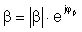
![]() (5.7)
(5.7)
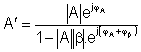
![]() (5.8)
(5.8)
Zosilnenie pre takúto spätnú väzbu vypočítame zo vzťahu:
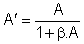
![]() (5.9)
(5.9)
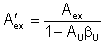
![]() (5.10)
(5.10)
Aex - je externý prenos napätia zosilňovača bez spätnej väzby
AU - je napäťové zosilnenie zosilňovača bez spätnej väzby
ßU - je napäťový prenos spätnoväzobného člena.
5.2 Stabilita so zápornou spätnou väzbou
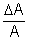
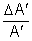
![]() (5.11)
(5.11)
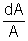
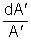
![]() (5.12)
(5.12)
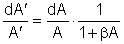
![]() (5.13)
(5.13)
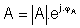
![]() (5.14)
(5.14)
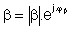
![]() (5.15)
(5.15)
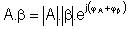
![]() (5.16)
(5.16)
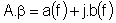
![]() (5.17)
(5.17)
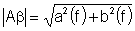
![]() (5.18)
(5.18)
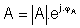
![]() (5.19)
(5.19)
Obr. 5.4 Nyquistova charakteristika
-ak všetky body frekvenčnej charakteristiky sústavy ležia vľavo od bodu [1,0], hovoríme o stabilnej sústave
-ak aspoň jeden bod frekvenčnej charakteristiky sústavy leží vpravo od bodu [1,0], hovoríme o nestabilnej sústave.
5.3 Skreslenie so zápornou spätnou väzbou
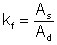
![]() (5.20)
(5.20)
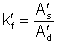
![]() (5.21)
(5.21)
Ad - je zosilnenie zosilňovača bez spätnej väzby pre dolné frekvencie
A'S - je zosilnenie zosilňovača so spätnou väzbou pre stredné frekvencie
A'd - je zosilnenie zosilňovača so spätnou väzbou pre dolné frekvencie
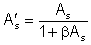
![]() (5.22)
(5.22)
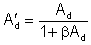
![]() (5.23)
(5.23)
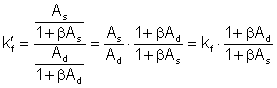
![]() (5.24)
(5.24)
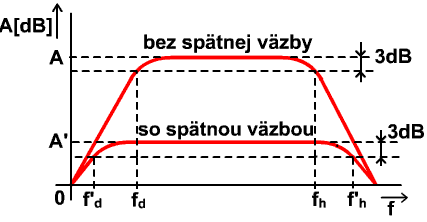
Obr. 5.5 Amplitúdová frekvenčná charakteristika zosilňovača so spätnou väzbou a bez nej
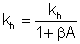
![]() (5.25)
(5.25)
- činiteľ harmonického skreslenia bez spätnej väzby kh < 10 %
- pomer medzi jednotlivými harmonickými zložkami nie je veľký
- zosilňovač pracuje v oblasti stredných kmitočtov, kde sa jedná o čistú zápornú spätnú väzbu
5.4 Vstupná a výstupná impedancia
Ak ide o sériovú spätnú väzbu, potom pre vstupnú impedanciu platí:
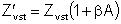
![]() (5.26)
(5.26)
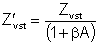
![]() (5.27)
(5.27)
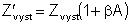
![]() (5.28)
(5.28)
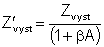
![]() (5.29)
(5.29)